PPE: A GraphEM-based Reconstruction#
Expected time to run through: ~0.5 hrs
In this section, we illustrate the basic workflow of the Graphical Expectation-Maximization algorithm (GraphEM, Guillot et al., 2015) with cfr, conducting a pseudoproxy experiment (PPE) with the pseudoPAGES2k dataset. Due to the intensive computational requirement of the GraphEM method, our goal is to reconstruct the air surface temperature field only over the tropical Pacific region using coral records.
Required data to complete this tutorial:
iCESM simulated air surface temperature: tas_sfc_Amon_iCESM_past1000historical_085001-200512.nc
iCESM simulated precipitation rate: pr_sfc_Amon_iCESM_past1000historical_085001-200512.nc
pseudoPAGES2k: ppwn_SNRinf_rta.nc
Note: pip install "cfr[graphem]" to enable the GraphEM method if not done before.
[1]:
%load_ext autoreload
%autoreload 2
import cfr
print(cfr.__version__)
import numpy as np
2023.7.21
GraphEM steps#
Create a reconstruction job object cfr.ReconJob and load the pseudoPAGES2k database#
A cfr.ReconJob object takes care of the workflow of a reconstruction task. It provides a series of attributes and methods to help the users go through each step of the reconstruction task, such as loading the proxy database, loading the model prior, calibrating and running the proxy system models, performing the data assimilation solver, etc.
[2]:
# create a reconstruction job object using the `cfr.ReconJob` class
job = cfr.ReconJob()
# load the pseudoPAGES2k database from a netCDF file
# load from a local copy
# job.proxydb = cfr.ProxyDatabase().load_nc('./data/ppwn_SNRinf_rta.nc')
# load from the cloud
job.load_proxydb('pseudoPAGES2k/ppwn_SNRinf_rta')
# filter the database
job.filter_proxydb(by='ptype', keys='coral')
# plot to have a check of the database
fig, ax = job.proxydb.plot(plot_count=True)
ax['count'].set_xlim(800, 2000)
[2]:
(800.0, 2000.0)
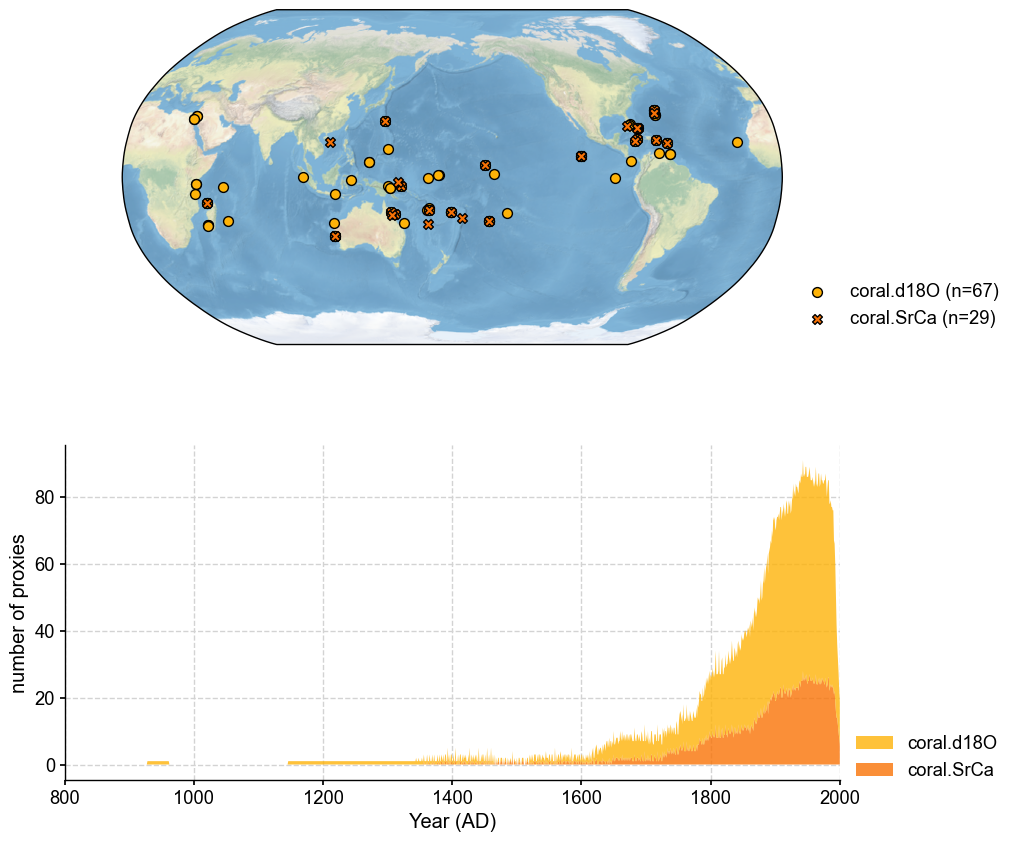
Annualize each proxy record#
[3]:
job.annualize_proxydb(months=list(range(1, 13)), verbose=True)
>>> job.configs["annualize_proxydb_months"] = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
>>> job.configs["annualize_proxydb_ptypes"] = {'coral.d18O', 'coral.SrCa'}
Annualizing ProxyDatabase: 100%|██████████| 96/96 [00:01<00:00, 48.59it/s]
>>> 96 records remaining
>>> job.proxydb updated
Center each proxy record#
GraphEM requires that the proxy availability to be as uniform as possible, we thus filter the proxy database further to achieve that.
[4]:
pdb = job.proxydb.copy()
pobj_list = []
recon_period = [1801, 2000]
for pobj in pdb:
if np.min(pobj.time) <= recon_period[0]:
pobj_list.append(pobj)
new_pdb = cfr.ProxyDatabase()
new_pdb += pobj_list
job.proxydb = new_pdb
fig, ax = job.proxydb.plot(plot_count=True)
ax['count'].set_xlim(*recon_period)
[4]:
(1801.0, 2000.0)
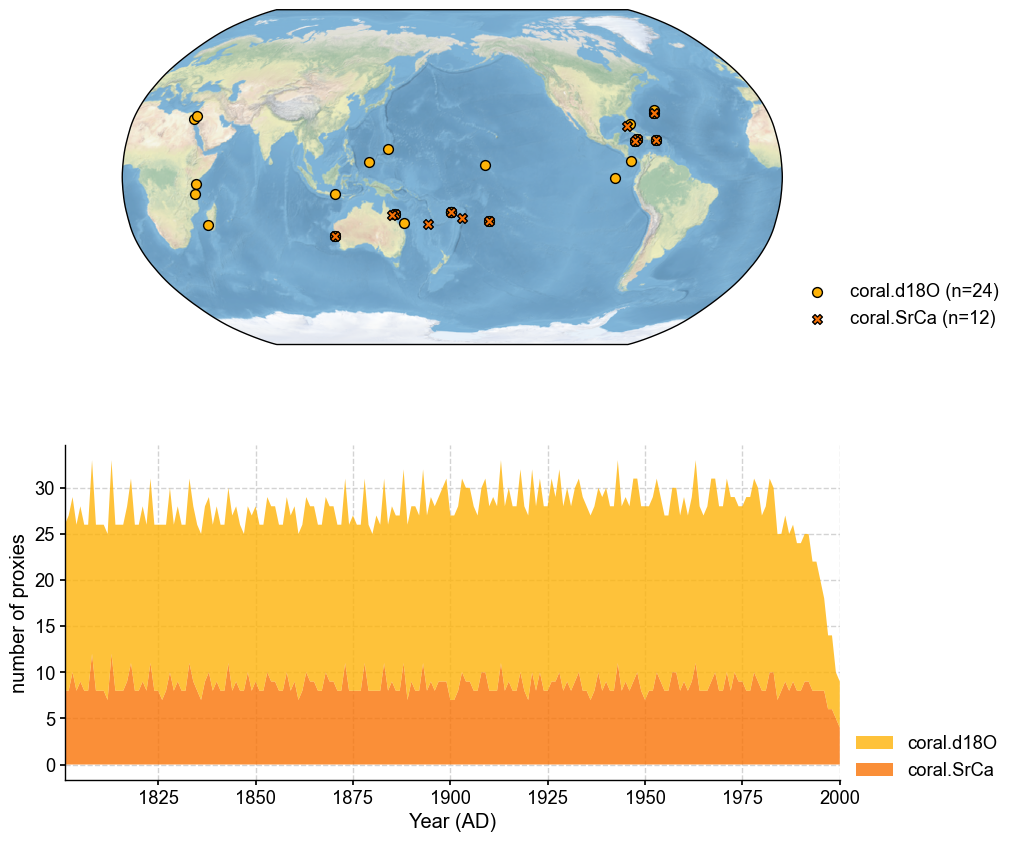
Load the instrumental observations#
As a perfect model prior pseudoproxy experiment (PPE), we use the iCESM simulated fields as instrumental observations.
[5]:
job.load_clim(
tag='obs',
path_dict={
# 'tas': './data/tas_sfc_Amon_iCESM_past1000historical_085001-200512.nc', # load from a local copy
'tas': 'iCESM_past1000historical/tas', # load from the cloud
},
anom_period=(1951, 1980),
load=True, # load the data into memeory to accelerate the later access; requires large memeory
verbose=True,
)
>>> job.configs["obs_path"] = {'tas': 'iCESM_past1000historical/tas'}
>>> job.configs["obs_anom_period"] = [1951, 1980]
>>> job.configs["obs_lat_name"] = lat
>>> job.configs["obs_lon_name"] = lon
>>> job.configs["obs_time_name"] = time
>>> The target file seems existed at: ./data/tas_sfc_Amon_iCESM_past1000historical_085001-200512.nc . Loading from it instead of downloading ...
>>> obs variables ['tas'] loaded
>>> job.obs created
Annualize the observation fields#
This step will determine the temporal resolution of the reconstructed fields.
[6]:
job.annualize_clim(tag='obs', verbose=True, months=list(range(1, 13)))
>>> job.configs["obs_annualize_months"] = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
>>> Processing tas ...
>>> job.obs updated
Regrid the observation fields#
This step will determine the spatial resolution of the reconstructed fields.
[7]:
job.regrid_clim(tag='obs', nlat=42, nlon=63, verbose=True)
>>> job.configs["obs_regrid_nlat"] = 42
>>> job.configs["obs_regrid_nlon"] = 63
>>> Processing tas ...
Crop the observations fields to make the problem size smaller#
[8]:
job.crop_clim(tag='obs', lat_min=-25, lat_max=25, lon_min=120, lon_max=280, verbose=True)
>>> job.configs["obs_lat_min"] = -25
>>> job.configs["obs_lat_max"] = 25
>>> job.configs["obs_lon_min"] = 120
>>> job.configs["obs_lon_max"] = 280
>>> Processing tas ...
[9]:
# check the cropped domain
fig, ax = job.obs['tas'][0].plot()
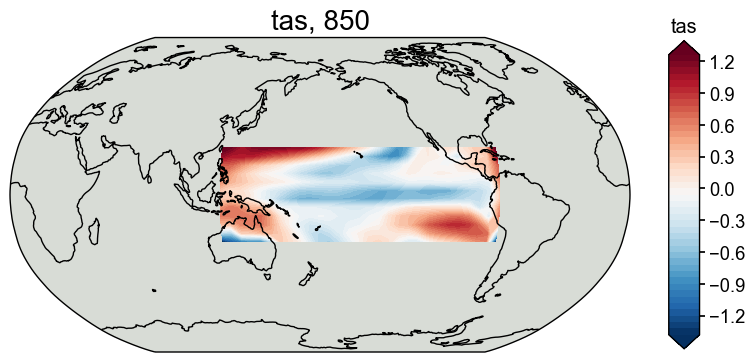
(Optional) Save the job object for later reload#
Save the job object before running the DA procedure for a quick reload next time if needed.
[11]:
job.save('./cases/pp2k-ppe-graphem', verbose=True)
>>> job.configs["save_dirpath"] = ./cases/pp2k-ppe-graphem
>>> obs_tas saved to: ./cases/pp2k-ppe-graphem/obs_tas.nc
>>> job saved to: ./cases/pp2k-ppe-graphem/job.pkl
Now let’s reload the job object from the saved directory.
[12]:
job = cfr.ReconJob()
job.load('./cases/pp2k-ppe-graphem/', verbose=True)
>>> job is loaded
>>> job.obs["tas"].da is loaded
Prepare the GraphEM solver#
[13]:
job.prep_graphem(
recon_period=(1801, 2000), # period to reconstruct
calib_period=(1901, 2000), # period for calibration
verbose=True,
)
>>> job.configs["recon_period"] = [1801, 2000]
>>> job.configs["recon_timescale"] = 1
>>> job.configs["calib_period"] = [1901, 2000]
>>> job.configs["uniform_pdb"] = True
>>> ProxyDatabase filtered to be more uniform. 35 records remaining.
>>> job.configs["proxydb_center_ref_period"] = [1901, 2000]
Centering each of the ProxyRecord: 100%|██████████| 35/35 [00:00<00:00, 2449.62it/s]
>>> job.proxydb updated
>>> job.graphem_params["recon_time"] created
>>> job.graphem_params["calib_time"] created
>>> job.graphem_params["field_obs"] created
>>> job.graphem_params["calib_idx"] created
>>> job.graphem_params["field"] created
>>> job.graphem_params["df_proxy"] created
>>> job.graphem_params["proxy"] created
>>> job.graphem_params["lonlat"] created
Run the GraphEM solver#
We will take the Empirical Graphs (graphical lasso, glasso) approach.
[14]:
job.run_graphem(
save_dirpath='./recons/pp2k-ppe-graphem',
graph_method='glasso',
verbose=True,
)
>>> job.configs["compress_params"] = {'zlib': True}
>>> job.configs["save_dirpath"] = ./recons/pp2k-ppe-graphem
>>> job.configs["save_filename"] = job_r01_recon.nc
>>> job.configs["graph_method"] = glasso
Applying the graphical lasso
Infilling missing values over the calibration period using RegEM iridge
EM | dXmis: 0.0008; rdXmis: 0.0072: 100%|██████████| 200/200 [22:06<00:00, 6.63s/it]
Solving graphical LASSO using greedy search
graph_greedy_search | FF: 3.767; FP: 3.036; PP: 2.689: 1%|▏ | 7/500 [00:01<01:39, 4.96it/s]
Running GraphEM:
EM | dXmis: 0.0018; rdXmis: 0.0047: 9%|▉ | 18/200 [04:38<46:52, 15.45s/it]
GraphEM.EM(): Tolerance achieved.
>>> job.graphem_solver created and saved to: None
>>> job.recon_fields created
>>> Reconstructed fields saved to: ./recons/pp2k-ppe-graphem/job_r01_recon.nc
Validation steps#
Create the reconstruction result object cfr.ReconRes.#
A cfr.ReconRes object takes care of the workflow of postprocessing and analyzing the reconstruction results. It provides handy methods to help the users load, validate, and visualize the reconstruction results.
[10]:
res = cfr.ReconRes('./recons/pp2k-ppe-graphem', verbose=True)
>>> res.paths:
['./recons/pp2k-ppe-graphem/job_r01_recon.nc']
Load the reconstructed variables#
Here we validate the tas field and the NINO3.4 index as an example.
[11]:
res.load(['tas', 'nino3.4'], verbose=True)
>>> ReconRes.recons["tas"] created
>>> ReconRes.da["tas"] created
>>> ReconRes.recons["nino3.4"] created
>>> ReconRes.da["nino3.4"] created
Validate the reconstructed NINO3.4#
We calculate the annualized NINO3.4 from the “instrumental observations” as a reference for validation.
[12]:
ref = job.obs['tas'].index('nino3.4')
We use a chain calling of several methods, including the validation step .validate() and the plotting step .plot_qs().
[13]:
fig, ax = res.recons['nino3.4'].compare(ref, timespan=(1801, 1900)).plot_qs()
ax.set_xlim(1800, 2000)
ax.set_ylim(-2, 3)
[13]:
(-2.0, 3.0)
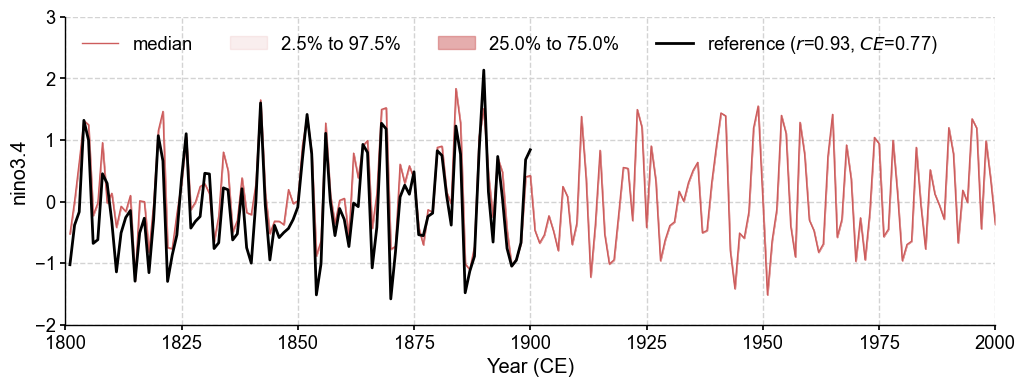
Validate the reconstructed fields#
[14]:
stat = 'R2'
valid_fd = res.recons['tas'].compare(
job.obs['tas'], stat=stat,
timespan=(1801, 1900),
)
valid_fd.plot_kwargs.update({'cbar_orientation': 'horizontal', 'cbar_pad': 0.1})
fig, ax = valid_fd.plot(
title=f'{stat}(recon, obs), mean={valid_fd.geo_mean().value[0,0]:.2f}',
projection='PlateCarree',
latlon_range=(-25, 25, 120, 280),
plot_cbar=True,
plot_proxydb=True, proxydb=job.proxydb,
proxydb_lgd_kws={'loc': 'lower left', 'bbox_to_anchor': (1, 0)},
)
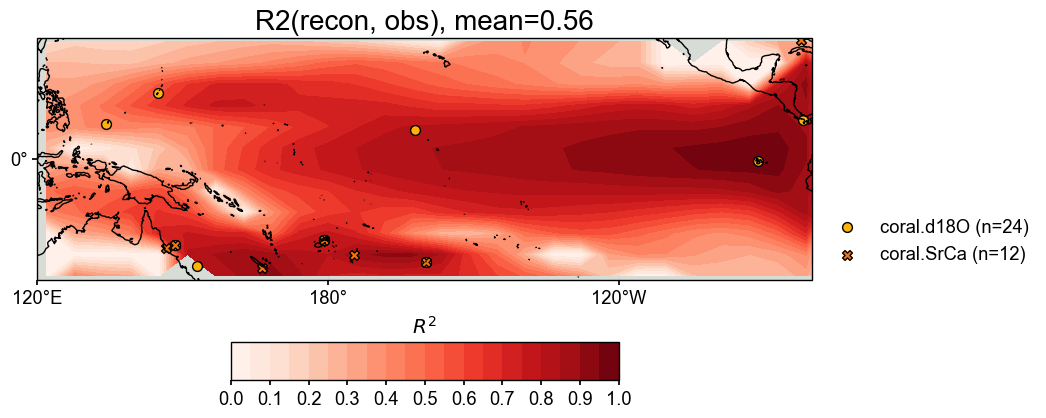
Note that there are regions where color is not filled. The values there are NaNs, and it is caused by the constant values in the reconstruction.
[15]:
res.recons['tas']['1801':'1900'].da[:, 0, 0]
[15]:
<xarray.DataArray 'tas' (time: 99)>
array([-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978, -0.02863978,
-0.02863978, -0.02863978, -0.02863978, -0.02863978])
Coordinates:
* time (time) int64 1801 1802 1803 1804 1805 ... 1895 1896 1897 1898 1899
lat float64 -24.15
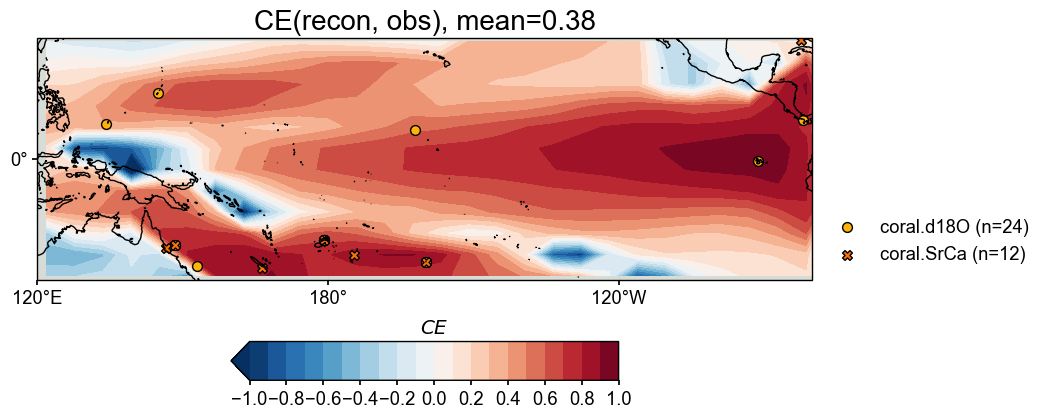
lon float64 121.9In contrast to \(R^2\), the coefficient of efficiency (\(CE\)) measures not only the linear correlation between two timeseries, but also the bias in amplitude. Calculating and visualizing \(CE\) between the reconstructed and the target fields, we see overall similar spatial patterns of the high and low skill regions.
[16]:
stat = 'CE'
valid_fd = res.recons['tas'].compare(
job.obs['tas'], stat=stat,
timespan=(1801, 1900),
)
valid_fd.plot_kwargs.update({'cbar_orientation': 'horizontal', 'cbar_pad': 0.1})
fig, ax = valid_fd.plot(
title=f'{stat}(recon, obs), mean={valid_fd.geo_mean().value[0,0]:.2f}',
projection='PlateCarree',
latlon_range=(-25, 25, 120, 280),
plot_cbar=True,
plot_proxydb=True, proxydb=job.proxydb,
proxydb_lgd_kws={'loc': 'lower left', 'bbox_to_anchor': (1, 0)},
)
[ ]:
